I'll
Give You a Definite Maybe
An Introductory Handbook to
Probability, Statistics and Excel
[This text has been prepared by Ian Johnston of Malaspina University-College, Nanaimo, BC, for the use of students in Liberal Studies. The text is in the public domain, released May 2000, and may be used, in whole or in part, without permission and without charge, provided the source is acknowledged]
For comments, suggestions, corrections, improvements, and what not, please contact Ian Johnston
Section Three: Descriptive Statistics, Histograms
In this module we consider some of the basic ways in which a researcher treats a collection of mathematical results (scores) from a test or research project. Of particular importance here is the definition of the following basic statistical concepts: mean, histogram, frequency distribution, variance, standard deviation, z-score. These terms may sound forbidding at first, but by the end of this module you should be quite familiar with them. And you should not proceed beyond this module until you can use the terms fluently and accurately.
To follow these pages properly you will need to be working with an Excel Worksheet open in front of you. In this way, you should be extending your command of Excel while exploring the world of basic descriptive statistics.
A. Introductory Terms: Distribution, Range, Median, Mode, Mean
The term statistics refers, very generally, to the collection, description, and analysis of numerical information (data). The data might be a collection of measurements of some physical characteristic (e.g., height, weight, pulse rates, angles, temperatures, linear measurements), test scores, performance results, incomes, answers to a questionnaire, and so on. The first step in any statistical study (after the design of the study, which may be very time consuming) is the collection of the mathematical information, the data. Once the information has been collected, the description and analysis can begin.
Let us set up our own small statistical exercise. In a fresh Excel worksheet, type in cell A1 the heading Scores. Then in cells A2 to A12 enter the following eleven numbers:
55, 75, 77, 68, 93, 64, 71, 83, 68, 69, 80
Sorting Data
This is our total number of results (our population). We call this set of results a distribution. To begin our description of the distribution, we often wish to arrange the scores in ascending or descending order of magnitude (rather than just in the order in which we recorded them). So let us first put these scores into an ascending order. Excel will arrange this quickly.
First select the range of cells A2 to A12 (the ones you want sorted). Remember that selecting cells involves putting the cursor in a corner cell, pressing down the left mouse button, holding it down, and dragging the cursor through the relevant cells. Then select from the menu at the top the Data option. From the drop down menu, select Sort. The Sort option chart which then appears should need no adjustment if we want the data in ascending order. So all you should need to do is press the OK button (note that if you wanted the data in descending order, then you would click on the descending option in the lower left corner of the Sort box before clicking on OK).
Your original data should now be rearranged so that the lowest value is in A2 and the highest in A12.
Describing the Data
With the data now in order we can easily identify the high and low values in the distribution (55 and 93). These two figures give us the range of the distribution (i.e., the upper and lower limits of the results). We can also quickly locate the value which lies in the exact middle of the distribution, the figure which splits the series in half, with half the observed values coming above it and half below it. This middle figure in the above distribution is 71 (the sixth value, with five above and five below). This mid-point in the distribution is called the median.
If the number of observed values in the distribution is an even number, then there will be no single clear observed value exactly in the centre. In such a case the median is half way between the two mid-values. For example, in the following distribution, the number of observed values is even:
0, 16, 18, 20, 33, 48
The median here would be half way between the two middle values (18 and 20). To calculate that we add them up and divide by two: (18 + 20)/2, which equals 19. In this case the median of the distribution is 19 (even though there is no result which corresponds to that value).
A particularly useful descriptive value in any distribution is the arithmetical average of all the results. This value is called the mean. We calculate this by adding up all the values in the range and dividing by the number of separate observed values which make up the distribution.
We have already seen how we can instruct Excel to determine this value for us, either with a formula which adds up all the numbers and divides by the total of entries or simply by asking Excel with the word average.
Let us go through that process again. Select cell A14. In cell A14 enter the formula which will instruct Excel to calculate the mean and enter the figure on the worksheet. The formula, you remember, goes like this:
=Average(A2:A12)
The figure for the mean in this case is 73. Notice that in common speech when we use the word Average we normally are referring to the mean.
A third term we can easily derive from a numerical distribution of data is called the mode. This value is the most frequently appearing value in the distribution (i.e., the most popular). In the list of our eleven results all the values occur once, except 68, which appears twice. Hence, in this distribution 68 is the mode. A particular distribution may obviously have more than one mode. In such a case we say that the distribution has two (or three or four) modes.
In the small distribution we are dealing with, we can find the median and mode quickly by eye. But if we want Excel to do the work, we simply have to ask. For example, select cell A15, and enter the following formula:
=Median(A2:A12)
When you strike Enter, the number 71 (the median) will appear in cell A15. In the same way, select cell A16, and enter the following formula:
=Mode(A2:A12)
When you strike the Enter key, the number 68 (the mode) appears in cell A16. In a much longer distribution, where sorting out the median and the mode by eye is not quite so easy, the Excel functions are much faster.
The mean, the median, and the mode are three different descriptions of what we might call "averages" (although in common speech, as noted above, the word average normally refers only to the mean, the arithmetical average). But it is important to remember that they are not always the same. In the list of test scores we have been considering, for example, the mean is 73, the median 71, and the mode 68. In some distributions, as we shall see, the three values coincide.
The mean, the median, and the mode are three measures of what is called the central tendency of the distribution, which refers to the tendency of a distribution of scores to group around a particular value. However, one has to be careful to keep the distinctions between these three descriptive terms in mind, because they reveal different things and have different uses.
For example, notice that if we alter the high value in any list of numbers to make it much higher, the values of the median and mode would be unaffected; whereas, the value of the mean would change (increase).
B. Some Examples of Different "Averages"
A manufacturer of shoes has carried out a statistical study of the popularity of the different sizes of his product. The results (in terms of the sales figures for the different sizes regularly available) indicate the following in terms of thousands of items sold (no pun intended):
Size 7: 12
Size 8: 12
Size 9: 25
Size 10: 10
Size 11: 6
Size 12: 5
Size 13: 2
This gives a frequency distribution of the different sizes. Obviously the manufacturer's main interest here is in the most popular size, the most frequent value in the distribution, that is, the mode—Size 9. There would be little value in knowing the median, the middle value (Size 10), or in trying to calculate a mean for all the sizes sold (some sort of average number of sales per size).
Here is another example. Suppose the following list represents the annual earnings of all those working in a small factory. The management salaries are in bold and a larger font, and the figures are ranked in descending order
$85,000
$73,000
$73,000
$50,000
$25,000
$25,000
$25,000
$23,000
$18,000
$15,000
$15,000
$15,000
$15,000
In any dispute over wages for the shop floor work force in this example, the description of the central tendency of the distribution of salaries might make a big difference to the apparent persuasiveness of the case. Management might, for example, argue that the mean (the arithmetical average of all the salaries) is $35,154, well above comparable wages in the industry. The shop floor workers might refer to the mode ($15,000) or to the median value ($25,000) in their argument that the wages paid were too low. In such arguments each party will often use the term average to refer to its figure; as listeners, we need to understand just which of the three averages the speaker is referring to. One's understanding of the various claims will depend upon keeping in mind just what these terms refer to and how they often do not tell us very much about the full distribution (1).
C. Self-Test on Mode, Median, Mean
Complete the following questions (use the Excel calculating functions if you need to).
1. The annual salaries of the 12 faculty members in the Department of Liberal Studies at Podunk College are $25,000, $28,800, $28,800, $28,800, $30,000, $30,000, $31,200, $32,400, $32,400, $33,600, $36,000, $67,000. Calculate the mean and the median annual salary of this distribution. Is one of them a better "average"? Why?
2. On December 31, 1995, ten babies were born in the Nanaimo Regional General Hospital. Their weights in pounds were 7, 8, 8, 6, 4, 9, 10, 11, 8, 9. Calculate the mean, median, and mode for this distribution. Compare the results.
For the answers check the last paragraphs in this section.
D. Dispersion of the Distribution: Histograms
The mean, median, and mode give us some measure of the central tendency in a list of numerical data, and the upper and lower figures for the range tells us the high and low scores. But in order to understand a set of statistical data more clearly we obviously require a sense of the way in which the measured values are spread out from the central tendency. For example, are the values almost all clustered around the middle, or are there some very low and very high vales. The range and various "averages" tell us something, but they do not describe accurately the distribution of the values.
This problem introduces a key idea. What we often most want to know about a distribution of numbers is the frequency of the various results (how many high scores, how many average scores, how many low scores, and so on).
Let us consider an example. We test two classes of students with the same examination, and we get the following result:
Class A: 68, 69, 67, 66, 70, 67, 69, 70, 66
Class B: 68, 41, 46, 95, 53, 78, 83, 58, 90
These two distributions have the same mean (average) and median (68), but they are obviously different results. All students in Class A are passing with reasonably satisfactory but not outstanding marks; some students in Class B are failing badly, and some are doing very well. Obviously in these two populations the marks are distributed very differently.
Make sure you understand this concept of a distribution of scores. The concept refers to the way in which a number of test results (numbers) are scattered through a particular range. If you like, you can think of the term distribution as referring to the pattern of results (e.g., all closely clustered together, some very high and very low scores at either end of the set of numbers, a cluster of high scores and a cluster of very low scores, evenly spaced throughout a wide range, and so on).
One way we can describe the distribution of a set of results is with a simple diagram which enables us immediately to see a particular shape or pattern to the distribution. Such a diagram is called a histogram, an extremely common feature of statistics.
Here's a very simple example. We have the following distribution which we wish to represent visually:
11, 11, 9, 9, 9, 8, 7, 6, 5, 5
To convert this numerical series into a histogram, we draw a horizontal line representing the values of all the numbers and a x above the appropriate number along the line, as follows:
| x | ||||||||||||
| x | x | x | ||||||||||
| x | x | x | x | x | x | |||||||
|
-------------------------------------------------------------------------------------------------------------------------------------------- |
||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
Every value in the original distribution is represented with an x above the appropriate number (hence, there is one x for values 6, 7, and 8, because they each occur once in the distribution; there are two x's for 11 and 5 and three x's for 9). What this means (and this is a key concept) is that the frequency of any particular value is directly indicated by the height of the column of x's above the value. We know at a glance that 9 is the most frequent value in the distribution because the column of x's above the figure 9 on the horizontal scale is higher than any other column. Please make sure you understand this idea very clearly.
In practice, a diagrammatic representation of the frequency of the values in a distribution is not made with x's but with vertical rectangles. The following chart represents how the data above would be normally represented.
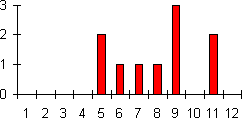
This diagram is essentially the same as the one we constructed above with the horizontal line and x's. But it is more complete. The horizontal line (the X axis) still indicates the values we are interested in. And the vertical line on the left (the Y axis) indicates the frequency. Thus we can see from the shape of the rectangles (the height) the relative frequency of each value. The higher the rectangle, the more frequent the value.
Such a diagram is called a histogram. It tells us visually about the frequency of the values in a distribution. The highest rectangle indicates the most frequent values; the lowest rectangles indicate the least frequent values; where there are no rectangles at all, there are no results corresponding to those values (e.g., 1, 2, 3, 4, 10, 12). Rectangles of equal height indicate that the values they represent occur in the same frequency (e.g., 6, 7, and 8 in the above diagram, each of which occurs once in the frequency distribution).
Notice also two very important standard characteristics of a histogram: the further to the right a rectangle occurs on the X-axis (the horizontal line) the higher the value it represents; the higher a column stands, the more frequent that value in the distribution (these points are fundamental to understanding what follows).
The shape of a histogram will always be determined by the nature of the data it represents. Hence, the shapes of histograms may vary enormously. With a little practice you will soon be able from a quick inspection of a histogram to describe some important features of a distribution.
E. Self-Test on a Simple Reading of a Histogram
Below are a number of different histogram shapes, each representing a different distribution. Translate the shape into a verbal description of the frequency distribution. Is there a pattern discernible? What are the least frequent values and where do they occur? What about the most frequent values? Can you make an educated guess about where the mean value for the distribution is likely to occur and its relative frequency (i.e., just from a visual inspection of the histogram can you estimate what the average score in this distribution is likely to be and how frequent that score will be)?
Here is the first example. We will review it, and then you can go on to examine the others.
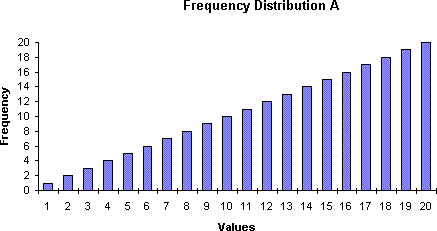
In this distribution we can see that the values range from 1 to 20 (the values given on the X-axis). The frequency of the values increases steadily as the values increase; we can see that by the steadily increasing height of the rectangles as we move to the right across the diagram. The most frequent values are the highest (the values corresponding to 20); the least frequent values (i.e., the lowest rectangles) occur on the left end, indicating that these least frequent results are also the lowest values.
The mean here will fall somewhere between the tallest column and the middle column. Its value is thus closer to the higher end (the right hand side of the histogram). Its frequency (indicated by the height) will be relatively high.
Make sure you understand clearly the visual information presented by such a histogram, in particular, that the values of the scores are indicated by the horizontal X-axis, that the frequencies of the scores by the vertical Y-axis, and that the frequency of any particular value will thus be indicated by the height of the rectangle above it. Make sure also you understand the point that as one moves to the right of the histogram, the values of the scores increase and that as one moves up the diagram the value of the frequency increases.
Try to provide similar descriptions for the following histograms. You can check the answers provided at the end of this section.

F. A Measure of the Distribution: Variation and Standard Deviation
Diagrams (histograms) are very useful depictions of a distribution, but statisticians want more accurate mathematical ways to describe the distribution. We have already dealt with some preliminary mathematical expressions like the mean, mode, median, and range, but, as we have seen, these provide only limited information about the details of the distribution of numbers.
To obtain a more useful mathematical expression of the shape of a distribution, mathematicians have devised the concept of Variation to measure how closely the values in a distribution are to the mean (the arithmetical average). The Variation is calculated as follows:
1. First, we calculate the mean of all the figures in the distribution (as before, adding them up and dividing by the number of separate entries or, more quickly, by entering the figures into an Excel worksheet and asking Excel to calculate the mean).
2. Then, we subtract the mean from each of the scores in turn. This will give us a separate result for each of the figures in the distribution, each result indicating how far that particular value is from the mean of the distribution. And some of the results will be negative numbers, since some of the observed results will be less than the mean for all the results.
3. Then, we square each value calculated in the previous step (i.e., multiply it by itself) (and remember that squaring a negative number always produces a positive number, so that -22 and +22 produce the same result: 4.
4. Having calculated each value in Step 3 above, we then add up these figures and divide by the number of entries in the range of values. This average we obtain is called the Variation.
Since the figures which go into the calculation of the Variation take into account the distance of each value from the average (the mean), the Variation is a measure of the extent to which the distribution is bunched near the mean (a small Variation) or extended through a wider range (a larger Variation).
G. Exercise in Calculating Variation
Let us go through an exercise in calculating the Variation of a distribution, using Excel to make the calculations easier. Open up a fresh worksheet in Excel (by clicking on the word File at the top left, selecting the Close option, clicking on the No option when Excel asks if you want to save the result, and selecting the New option). Then enter the following numbers (the results of a personnel test we have administered).
11, 11, 9, 9, 9, 8, 7, 6, 5, 5
1. First in cell A1 of the Excel worksheet, type in the heading Scores. Then, in Column A, starting in A2, list the above scores. This will take up the cells from A2 to A11.
2. Now, we have to calculate the mean of this distribution. Remember you can get Excel to do this very quickly. Select cell A13, and enter the following formula:
=Average(A2:A11)
Then strike Enter. The mean value (8) will appear in the cell you have selected (A13).
3. Now, in Column B we will carry out the second step in the calculation of the Variation, by subtracting the mean from each value in A. So in cell B1 type in the heading V-M (for value minus mean). Select Cell B2 and write in the formula indicating this step:
=A2-8
This formula is telling Excel to subtract 8 from the value in A2 and enter the result in cell B2.
4. We could repeat this formula for each value in Column B, but it is easier simply to copy the formula in cell B2 and apply it to the cells B3 to B11. Use the shortcut explained at the end of the previous section: select B2, place the cursor directly over the small square at the bottom right corner of the border around the cell (so that the cursor turns into a cross hair), press down the left mouse button, and holding the button down, drag the cursor down through the cells you want to contain the copied formula (i.e., cells B3 to B11). Then release the left mouse button.
Notice that the values now appear in the appropriate B cells, each value representing the corresponding value in the A column with 8 subtracted. Note, too that some of them are negative.
5. Now, for the third step we want to square each figure in column B. Start by putting in a heading in cell C1: Squares. Then in cell C2 put in the appropriate formula to carry out this calculation.
=B2*B2
This is telling Excel to enter in this square a value equal to the value in B2 multiplied by itself. Now, copy the formula, using the same process. Select C2, select Copy from the Edit menu, hold down the left mouse button, and drag the mouse through the cells C2, C3, C4, C5, and so on up to C11 (remember that you can use the shortcut: selecting C2, moving the mouse pointer over the small square in the bottom right hand corner of C2 until the mouse pointer turns into a cross hair, holding down the left mouse button, and then dragging the mouse, with the left button still held down, through the range of cells, down to C11).
6. Now, for the final step we need the mean value of the figures in Column C. We do this in the usual way. First, we select a cell where we want the mean to appear. So select cell C13. Then type in the appropriate formula:
=Average(C2:C11)
The figure which appears in cell C13 is the variation. If you have followed all the steps outlined above, that figure should be 4.4.
Notice that we can skip all these calculations and simply ask Excel to calculate the Variation for the original numbers we entered in Column A. For example, select cell C14, and enter the following formula:
=Var(A2:A11)
This formula is asking Excel to calculate the Variation for the numbers given in cells A2 to A11. If you strike Enter, you will see the figure 4.8889 (the number of decimal points will depend upon the settings on your computer).
You will notice immediately that this value of 4.8889 (or 4.9) is not the same as the one we arrived at in the detailed method. There is an important reason for this, which we need not bother about here in detail. What Excel has done in the last step (to determine the mean of the squared values) is to divide the total of the numbers by one less than the number of entries (i.e., by 9 rather than by 10).
Excel does this because it treats the numbers we have entered in Column A as a sample (i.e., a selection from a much larger population), and, when dealing with a sample, rather than with a full population, mathematicians have established that one obtains a more accurate measure of the Variation by doing this. We need not worry about the point at this juncture. We will be getting to samples later. For the moment we will be dealing with the value which we calculated ourselves: 4.4.
H. The Standard Deviation
We calculated the Variation by squaring the values we obtained by subtracting the mean from each value. In order to get back to a number which is not a squared value, we also use the square root of the Variation. This value is called the Standard Deviation.
Thus, if the Variation of the distribution we entered into Column A is 4.4, then the Standard Deviation is the square root of that figure. To calculate the square root, we simply ask Excel to give us the square root of 4.4. Select cell C15, and enter the formula
=sqrt(C13)
This is telling Excel to calculate the square root of the number in cell C13 and to enter the result in C15. When you strike Enter the number will appear (2.1).
This value, the Standard Deviation is an extremely important statistical concept, central to everything we do from now on. The essential point to remember is that the Standard Deviation is a measure of the extent to which a distribution is grouped around the average (the mean) or spread out away from the mean. The smaller the standard deviation in a distribution, the more all the values will tend to cluster around the mean; the larger the standard deviation the more the values will be distributed away from the mean.
For example, if the standard deviation for a distribution is exactly 0, that means that all the values in the distribution fall exactly on the mean (i.e., they are all the same). A set of numbers with a standard deviation value of 1 will be clustered closer to the mean (i.e., it will be a more bunched up distribution) than will a set of numbers with a standard deviation of 1.5 or 2, and so on.
I. Note on Decimal Places in Excel
You can adjust the number of decimal places (i.e., numbers after the decimal point) which Excel will display in a particular cell. The easiest way to do this is to select the cell (or the column of cells, if you wish to change many numbers at once) which you wish to change and then use one of the two buttons in the second line of the Toolbar. Notice the two buttons on the right side of the tool bar, each with some zeros on it, one with an arrow pointing to the left, and the other with a small arrow pointing to the right. If you click on the first button (the one with the arrow pointing to the right) you will increase the number of decimal places for the figure in that cell; if you click the mouse on the button with the arrow pointing to the right, you will decrease the number of decimal places.
J. A Short Cut to Descriptive Statistics Information
In this section we have gone through a number of calculations (with the help of Excel) to calculate various descriptive values: mean, mode, median, range, variance, and standard deviation. There is a very quick way to obtain all this information in one easy procedure, as follows.
In order to demonstrate this short cut, get rid of the worksheet we have been using for the previous exercise (there is no need to save it), and obtain a new worksheet.
For the sake of this exercise, let us assume that we have measured the weight (in pounds) of all members of a group and that we now wish to describe this distribution so that we can begin to compare the data with a similar set collected from another group. The values we collected (in pounds) were as follows:
123, 156, 210, 185, 146, 135, 168, 220, 167, 192, 134, 176, 196, 116, 140, 175
This is our information. Put in cell A1 the heading "Weights" and then enter the figures in the A column from cells A2 to A17.
Now, rather than going through separate requests for the Mean, the Mode, the Median, the Variation, and the Standard Deviation, we can ask for a table that will give all these figures (and more) in a single operation. We do this by the following process:
1. Point the mouse arrow onto the word Tools in the top menu, and click the left mouse button. From the drop down menu select Data Analysis. It will normally be the last item in the menu. If it is not there, then proceed to the next step. If Data Analysis is in the menu, put the mouse indicator on the word, click the left mouse button, and omit the next step.
2. If the Data Analysis option is not available on the Tools menu, then select instead the Add-ins option. Excel will take some time to bring up the Add-ins menu. When that appears, click the left mouse button when the mouse arrow is in the square to the left of the first item, Analysis ToolPak. That will add to the Tools Menu the option Data Analysis, so that you can go back to the Tools menu and select the Data Analysis (i.e., go back to Step 1 above).
3. When the Data Analysis Menu appears on the screen, point the mouse arrow to the term Descriptive Statistics (the sixth item on the list), and click the left mouse button. The screen will now present a Descriptive Statistics box which requires some information, as follows:
4. The first line, Input Range, is asking for the range of cells which contains the data you want included in the analysis. Select the range of cells you wish to describe. You can do this with the mouse by moving the mouse pointer into cell A2, holding the left mouse button down, and dragging the mouse through cells A3, A4, A5, and so on until we get to A17. Then release the left mouse button. The range of cells with the numbers in it has now turned dark (to indicate that it has been selected). Notice that the Input Range has in it the following symbols: $A$2:$A$17. Since you have already selected A2 to A17, that box will have in it the symbols $A$2:$A$17. The $ signs indicate that this is a range input.
Alternatively, you can type in the Input Range (without selecting the cells by dragging the mouse). Click the mouse pointer in the Input Range box and then type in the range: $A$2:$A$17 (do not forget the dollar signs).
5. Move the mouse pointer into the square to the left of the box in the lower half of the Descriptive Statistics menu, beside the label Output Range, which should be empty. Click the left mouse button with the arrow pointing in that box. In the Output Range box (the rectangle), you should enter the name of the cell where you want the Statistical Descriptive Data Table to start (the top left hand corner of the table). Then, in the box, type $A$18 (indicating that you want the top left corner of the table to be in cell A18). Alternatively, if you do not want to type anything in the box, simply move the mouse pointer to cell A18 and click it once. The symbols $A$18 will appear in the Output Range box.
6. Finally, make sure there is an x in the small square beside the label Summary Statistics. If there is no x in that box, then put one there by placing the mouse arrow in the box an clicking the left mouse button once.
7. When you have entered all that information in the Descriptive Statistics box, click on the OK button. There will be a short delay while Excel calculates the statistical information. When that process is completed, the data will appear in a block with the upper left hand corner in the designated place (cell A18)
8. The Descriptive Statistics box contains two columns. Notice that the column on the left is not wide enough for all the words to appear. To correct this, widen column A by moving the mouse pointer so that it sits exactly on the line separating the cell containing the letter A from the cell containing the letter B. When you do this, you will notice that the mouse pointer changes shape and becomes a line arrows pointing to the left and to the right. Press the left mouse button down and, still holding it down, move the mouse to the right. You will notice that, as you do this, you move the line separating Column A and Column B to the right. Move that line until it sits directly on top of the existing line between Column B and Column C. Then release the left mouse button. You see that Excel has now widened Column A so that it is twice a wide as it was before; there is now room for the full descriptive labels to appear.
The list of Descriptive Statistics gives us values for a number of different statistical measurements, some of which we are already familiar with (Mean, Mode, Median, Variance, Standard Deviation, Sum, Range, Count, Maximum, and Minimum). We have generated all these for the data we have entered in Column A with one operation, a much quicker procedure than going though the various calculations separately.
Before leaving this Descriptive Statistics table, we should look briefly at the unfamiliar labels.
The Standard Error is a very important value, which we will be meeting shortly. We will be making extensive use of it later, so for the time being just remember that we can find the Standard Error of a distribution by using the Data Analysis function in Excel.
The Skewness of a distribution, which we will not be concerned with, is a measure of how the overall results fall relative to the mean. If a distribution is symmetric, with equal frequencies on either side of the mean, the skewness in the distribution is 0. If the distribution is "skewed," so that it has a longer "tail" above the mean, then the distribution is skewed positively; if the longer "tail" is below the mean, the distribution will be skewed negatively.
The Kurtosis value of a distribution is a measure of the thickness of the extreme ends of the distribution (we will not be concerned with that in this module).
K. Self-Test on Standard Deviations and Excel Descriptive Statistics
Using the Excel Descriptive Statistics capability, compare the two following results. Which of them is the more widely distributed? Which of them has the higher mean? Use the Standard Deviation as calculated by Excel (even though that is, as we have seen, slightly higher than the normal calculation).
Population
A: 8, 9, 10, 11, 17, 12, 4, 10, 19, 25
Population B: 3, 9, 10, 11, 12, 8, 6, 13, 17, 9, 4
To carry out this exercise, enter the figures for the two populations in separate columns, and generate a different set of Descriptive Statistics for each set of results. You can do this on the same Worksheet, provided you make sure when you enter the Output Range cell (where you want the table of Descriptive Statistics to appear), you do not have the two tables overlapping.
For an answer to this self-test, see the last paragraphs in this section of the module.
L. One Important Use of the Standard Deviation
You have just received back two results from class tests: on the English test you scored a mark of 62 percent and on a History test you scored a mark of 80 percent. You would probably conclude that you had had much more success in the History test than in the English test. And on the basis of the raw scores, that does seem to be the case.
But supposing we are interested, not just in the raw score, but in your standing relative to the entire group (i.e., where did you stand in relation to the other students, rather than to a fixed objective standard?). This is an interesting statistic, because it describes your success in relation to your fellow students, your peers.
Suppose on the English test (in which you scored 62 percent) the class average (the mean) was 58, and the standard deviation was 2. Your mark of 62 is four marks above the average, and this 4 marks is equivalent to 2 standard deviations above the mean. This puts you well above the average.
Suppose on the History test (in which you scored 80 percent), the class average (the mean) was 65, and the standard deviation for the group was 10. Your mark is 15 above the mean, which is equivalent to 1.5 standard deviations (15 divided by 10 is 1.5). This result of 1.5 standard deviations above the mean is not so far above the average as the result in the English test (2 standard deviations).
Notice what this process reveals. Although your raw score in the History test was higher than the mark on the English test, relative to your class mates you did much better on the English test, because you stood higher in the distribution of marks for that group than you did in the distribution of marks for the History test (although your mark in the History test is higher).
The point illustrated in the above example provides the basis for an important way of measuring success in a group text: the idea of the z-score.
M. z-Scores
Using the Standard Deviation in the way described in the section above (when we compared the results of the English and History tests), has given rise to the concept called z-scores. These translate a raw score (like the percentage results on a test) into a value which indicates the score relative to the distribution in the group of scores.
As teachers or personnel managers, we are often more interested in the way a result compares to the others, rather than in the raw score itself. Hence, we often wish to convert a raw score on a placement test into a z-score. We can do this in the following way:
1. First, we calculate the average score for the entire set of scores (the mean). Then we subtract the mean from each score. This will give a positive result if the score is above the mean and a negative result if the score is below the mean.
2. Secondly, we divide the result obtained in Step 1 by the Standard Deviation for the entire set of scores (obtained from the Descriptive Statistics box).
3. The result, the z-score, will be positive or negative (positive for those scores above the mean, negative for those below the mean).
Note carefully that the z-score is a measure of how far (in Standard Deviations) the raw score is above or below the mean. A z-score of 0 indicates that the raw score fell exactly on the mean; a z-score of -1.5 indicates that the raw score fell exactly 1.5 Standard Deviations below the mean (well below average); a z-score of 2.1 indicates that the raw score fell 2.1 Standard Deviations above the mean (a very good result, well above average).
The value of the z-score is that it measures the score relative to the scores in the entire set of results and thus indicates something which the raw score does not.
In most of the statistical exercises we are going to do (as in most practical applications) the importance of a particular result lies in its relationship to the other scores rather than to any absolute standard. Hence, the z-score is a key concept in many statistical procedures (and we will be using it constantly in the remainder of this module).
N. Self-Test on z-Scores
Here are two results you obtained in different tests. Determine (using the method we went through in the previous section) your relative success in comparison to the groups who took the different tests. In which test did you score better relative to all those taking the test? Once again, you can check the answer in the final section at the end of this section.
In the first test (Test A) you scored a mark of 81. The mean of all scores was 75.5, and the Standard Deviation was 12.44 marks. In the second test you scored 75; the mean was 72, and the Standard Deviation was 2.5 marks.
See the paragraphs at the end of this section for an answer to this self-test.
O. Percentile Rank
Another common method of indicating the value of a raw score (like a percentage result on a test) by changing it into a comparative mark which indicates the standing of each mark relative to the entire group who took the test is something called the percentile rank. This indicates the percentage of scores for the entire group with fall below a particular score.
For instance, if your result is in the 78th percentile, that means that 78 percent of the class received marks lower than yours (and 22 percent received higher marks than yours); a result in the 23rd percentile means that 23 percent of the class received marks lower than yours (77 percent received marks higher than yours).
The percentile rank is often more useful than the raw score (especially in many academic testing procedures) because it provides a ranked comparative placement of a particular result which is independent of the difficulty of the test. Like the z-score, it indicates, not your raw score, but rather how well you did in comparison with all the others.
Note that if you want a column of results to be converted into a percentile ranking, Excel will do this very quickly. All you have to do, once the data is entered, is select from the Data Analysis menu (where you selected Descriptive Statistics before) the option Rank and Percentile. The menu will then ask for the Input Range (i.e., the list of data you wish to have organized into a percentile ranking) and the Output Range (i.e., where you want the table to appear). Remember that in Excel Range entries, you need to put a dollar sign before the letter and the number. The resulting table will then rank the data in order and assign a percentile number to each entry.
Percentile Rank is often an important tool in evaluating results of a large number of applicants who have written a particular test (e.g., the Law School Admissions Test or LSAT), where one of the qualifications in some schools is that a candidate must achieve a score in the top 5 percent or even higher.
In our introduction to Statistics, however, we are not going to concern ourselves with Percentile Rank. For us the z-score is a much more important comparative measure.
P. Basic Charting Functions in Excel
One important feature of Excel is its ability to convert statistical data into graphic illustrations easily. Here again, we are going into only a small part of the full range of what Excel can do, but in the course of this module we will be working our way through a few useful standard charting exercises.
In order to go through the basic steps in charting, let us work through a simple example of converting numerical data into an illustration. In this case, our data is the results of an exercise, Test 1; we have observations for ten people, as follows (the letters of the alphabet represent people's names):
ab: 77
bc: 67
cd: 88
de: 54
ef: 80
fg: 63
gh: 68
hi: 92
ij: 58
jk: 75
Select a new worksheet in Excel. In Cell A1 write in the heading Names, and in Cell B1 write in the heading Scores. Then in order enter the names in Column A and the corresponding scores in Column B. When you are finished, you should have something entered in all cells from A1 to B11. We are now ready to start charting.
Q. Using the ChartWizard in Excel
First, select the cells to be included in the chart, that is, from Cells A1 to B11 (including the titles). If you forget how to select cells, consult the section earlier where we discussed that. Once the cells have been selected, click the left mouse button on the ChartWizard, the button in the toolbar to the immediate right of the AZ sort buttons on the top row.
Once you click on the ChartWizard button, the mouse pointer will turn into a crosshair (only in earlier editions of Excel; in Excel 2000 the Chart Wizard Box will open immediately). Now you have to indicate where on the worksheet you want the chart to appear and how big you want it to be. So position the cross hair where you want the top left point of the chart to fall. Then, holding down the left mouse button, drag the mouse down and to the right. You will notice as you do this that you are creating a rectangle. When the rectangle is an appropriate size (i.e., fairly big), release the left mouse button.
The rectangle will now disappear, and the ChartWizard will start asking you for questions about the chart you want. To start with, the first question asks you to confirm that the range of cells indicated is the one you wish to base the chart upon. If you selected the cells properly at the start (A1:B11) properly, you need to make no corrections and just point the Mouse onto the Next button (note that, as before, Excel uses dollar signs to denote a range: $A$1:$B$11). If you need to make corrections in the initial ChartWizard description of the range, you can do so (just don't forget to include the dollar signs).
Once you have looked over the cell range, click on Next. ChartWizard will now give you a choice of fifteen different chart possibilities. One of them, you will notice, is coloured black. That is the version ChartWizard recommends for this set of data. So, unless you want to experiment at this stage, you do not need to change anything. Click the mouse arrow on Next.
Similarly, at the next stage, ChartWizard will present you with a number of options, with the recommended one highlighted. Simply click the left mouse button on Next, and keep going.
In Step 4 of the ChartWizard process, the menu will give you a small preview of the chart you are creating. If you like the way it appears, keep going. If you don't like the look of it and would like to make some changes, you can cancel the process, start the ChartWizard procedures again, and make different choices. Generally, you don't need to make any changes here, because you can always edit the finished product (changing things like colour, gridlines, and so on). Cancel the chart at this stage only if the basic design (bar chart, pie chart, or whatever) is clearly not what you want.
The next to last stage of the ChartWizard process asks you whether you want to add any labels to the chart: a title, a label for the X-axis (the horizontal axis), the Y-axis (the vertical axis). Try giving the chart the title Test Results, label the X-Axis Names of Students and the Y-axis Score. Then select the button Finish. The complete chart should now appear in the rectangle you created at the start of the process, right on the worksheet with the original figures in the columns.
In Excel 2000 the last question from the Wizard will ask you whether you want the chart directly on the worksheet or on a page of its own. And Excel will size the chart on the worksheet automatically (you can alter it later if you want).
R. Selecting and Experimenting with the Design of the Chart
Once you have completed the chart, you may want to experiment with other possibilities, just to check whether this format is the best for your document or else just to play around with Excel's possibilities. Before you start to that that, however, you had better save the worksheet, so that you can come back to the present state of the worksheet if you make a mistake. Saving in Excel is exactly like the process in other Windows programs (go to File Menu, select Save As, give the worksheet a name, select the a: drive, and click OK).
In order to being experimenting with the chart you have just created, first you have to select the chart. A selected chart has small solid black rectangles evenly spaced around the perimeter border of the entire chart (in the corners and half way along each side). If the rectangles are already there, that means the chart is already selected. If they are not there, the place the mouse pointer in the chart area and click the left button once. The solid black rectangles should appear.
In addition, if the chart has been selected, in the top right hand corner of the work sheet a small toolbar menu with five buttons and the heading Chart should appear (this occurs only in earlier versions of Excel). If the black rectangles are around a portion of the chart (and not the entire chart area) point the cursor into a blank area near the edges of the chart and click the left mouse button again. The entire chart should now be selected.
If you want to see how your data might look under other chart formats, then click the left mouse button on the small arrow on the button at the left of the small Chart Toolbar in the top right corner of the worksheet. A drop-down menu will appear. You can then click on any one of the many options there, and Excel will reconfigure your data to fit a different form of chart (e.g., 3-dimensional bar chart, pie chart, scatter diagram, and so on). In some cases, where the format of the chart is not suitable for the data, you may get no result.
If you find a chart format you prefer to the one in which you created the chart in the first place, then leave that new format in place.
While working with the Chart Toolbar, notice the button on the extreme right end. That will automatically add a legend you your chart (useful if you are showing more than one test result on the same chart). The second button from the right enables you to add or subtract the gridlines. Try it. The second button from the left on the Chart Toolbar produces the default chart, the one which Excel thinks is most appropriate for the data you have entered on the worksheet.
S. Saving a Chart on a Sheet Separate from the Entered Data
Up to this point, the chart is on the same worksheet as the data you entered originally (unless you have deleted the data). You can save the material in that form and, if you wish, print both the data and the chart together. Often, however, you will want the chart to appear on a sheet separate from the data you originally entered in columns. Hence, you may want to separate the chart from the worksheet. To do this, go through the following procedure.
First, select the worksheet information you want the chart to include (in the case of our example, this would be A1:B11 (i.e., the numerical data on which the chart is based, together with any titles or names you have included in the chart). Then point the mouse arrow and the Insert menu (in the top row), click the left mouse button, and from the drop-down menu choose the Chart option. From the small menu which then appears, select As New Sheet option. From that point on you follow the ChartWizard instructions as before.
When you have completed the five steps of the ChartWizard, the chart will appear by itself, without the worksheet data on the same page.
With this procedure, the entered data and the chart will be separate documents, a useful process if you want to print only the chart (without the columns of data). However, if you want to save the chart for later work, do not forget to save the worksheet separately as well (for details on saving the chart, see the details immediately below).
T. Saving and Editing a Chart
Once you have created the chart on its own page you can save it separate from your original document (the worksheet). Simply go to the File option on the main menu at the very top left of the screen, and save the document as usual (with the Save As option from the drop-down menu. Excel gives your chart a name (Chart 1, Chart 2, and so on), but you can change that on the Save As menu, if you wish a different name. Make sure you save the chart as soon as have created it and before you start editing it, and save it again after every significant alteration. It's easy to lose a chart in the middle of some operation, so you want to have available what you have done already.
It is possible to edit a chart extensively. There is not space here to go into all the various options. However, we can review a few of the major changes, and playing around with a sample chart will indicate lots of other options. The basic procedure requires you to select a part of the chart which you wish to alter and then from the appropriate menu to select a different option. Selecting a part of the chart involves pointing with the mouse arrow to the appropriate part and clicking the left mouse button. A series of small solid rectangles and a perimeter line will indicate the part you have selected.
Suppose, for example that you wish to give your chart a title and to label the X and Y axes (if you have not done that in the ChartWizard process) or to change the names which are already there. First select the entire chart by pointing the mouse arrow up near the upper left corner of the chart. A series of black solid squares should appear around the perimeter of the entire chart and there should be a line around the entire chart area. Once you have selected the entire chart, point the mouse arrow to the Insert option on the top menu line of the screen, click the left mouse button, and from the drop-down menu select the appropriate options, which include a Title for the whole chart, labels for the X-axis and the Y-axis. You can choose which labels you like. (Note that in Excel 2000 you carry out such steps by going through the Chart Wizard again, after clicking on Insert and selecting Chart. Step 3 of the Chart Wizard deals with labels for the X and Y axes and a title for the entire chart).
Note that if you want to alter the font style or size, the colour, or the alignment of any text in the chart (like the title and the axis labels), double click the left mouse button on the particular text you wish to edit. That will give you the Format Chart Area box. By choosing Font or Alignment or Patterns you can select from among a number of options to create the style of text you want.
Correcting a Mistake Quickly
If you make a change which you do not like, you can immediately change it by pointing the mouse arrow to the Edit menu in the top line of the screen, clicking the left mouse button, and selecting the first item on the list, which will normally be an option to Undo what you have just done to the chart. This option only works on the last operation you completed, so that you cannot correct something you did two or three commands before. However, it is a useful way of dealing with any sudden changes which occur and which you do not wish to keep.
If you wish to edit the text to correct a misspelling or to change a label, then simply select that part of the chart and move the mouse into the box defined by the signs indicating what you have selected. The mouse pointer will become a vertical line which you can insert anywhere in the text. Then make the changes you wish.
You can also edit the colour of the columns. Begin by selecting the columns by pointing the mouse arrow into any one of them and clicking the left mouse button on that area. The small solid squares should now appear in some of the columns, indicating that they have been selected for editing. The click the mouse on the Format option on the top menu, and select the first item, Selected Data Series. From the box which appears, select Patterns. You will then be given a rich choice of alternative colours. This menu will indicate the colour presently on the chart and a range of options.
You can also put a border around any part of the chart or around the entire chart. Suppose we want to do the latter. First select the entire chart by pointing the mouse to the upper right of left corner of the chart, away from the middle of the chart but still in the chart area, and clicking the left mouse button. The series of squares which indicates what has been selected now lies on the outer perimeter of the chart (if the series does not lie there but in the interior of the chart, then in making your selection you have not pointed the mouse arrow far enough away from the centre of the chart, so keep doing that until the selected area is the entire chart).
Now from the Format drop-down menu, select Selected Data Series (or Selected Chart Area), and then Patterns. On the Patterns menu click the mouse on the circle beside the word Automatic on the left. Then click on the OK button. You will notice the chart now has a border around its outside perimeter. In the same way you can put a border around the title (selecting the title rather than the entire chart) or around the labels for the X-axis and the Y-axis.
If you wish to print the chart, select from the File drop down menu the Print command, just as you would in a word processing document. Note that if the chart represents a great deal of information it may take some time for the printer to produce the result. Also, in complex charts, processing a great deal of information, you will need a printer with a larger than normal memory. This will not normally be a problem with college laser printers, but if your printer at home simply refuses to print the document, the reason may be that it does not have enough memory.
When you wish to leave the chart to return to your worksheet, then from the File drop down menu select Close. Excel will ask you whether or not you wish to save the chart. Make sure you do.
Then, if you have not saved your original worksheet, Excel will ask you whether you want the chart saved with reference to unsaved documents. You can do this, provided that you save the Worksheet before you quit. If you do not save the worksheet, then when you go to Open the chart again, it may be blank (lacking any columns) because the numerical data which determine the columns is no longer available (you didn't save it). This point obviously does not apply when the chart and the numerical data are on the same worksheet and you are saving them both together.
Once you have saved the chart, Excel will return you to the original worksheet. Note that if you make any changes to the numerical data on this worksheet, these changes will be reflected in the chart when you next open it. The chart, in other words, is still dependent on the data you enter.
Moving Back and Forth From Chart to Worksheet
If you created the chart on a separate page from the data, you can move back and forth between the chart and the data by clicking on the tabs at the bottom of the worksheet (the tabs called Chart 1, Chart 2, Chart 3 and Sheet 1, Sheet 2, Sheet 3).
If you created the chart on the same page as the entered data (on the original worksheet) then you can move from chart to data and back again with the cursor or the arrow keys.
Sizing the Chart
You can easily alter the dimensions of any chart. First select the entire chart, so that the black rectangles are on the outer perimeter. To make the chart taller, position the cursor directly over the black rectangle half way along the top border line of the chart. The cursor will change into a double arrow. Hold down the left mouse button and move the mouse up. You notice that a dotted line indicates the new top border of the chart. When you release the mouse button, the chart will take on the new dimensions.
You can use the same procedure to make the chart wider (working with the rectangle on one of the sides). And, of course, you can make the chart smaller as well, using the same technique.
U. Adding Data to an Existing Worksheet and Chart
Now, suppose we have a second set of Test results for the same class and we want to enter these onto the chart as well, so that we have a visual comparison of the two sets of results. You should still have the scores from the first test in Column A (if you have erased them, then re-enter them). Here are the results for the second set of scores:
ab: 83
bc: 50
cd: 75
de: 67
ef: 85
fg: 72
gh: 68
hi: 88
ij: 63
jk: 70
First, we enter these on our original Excel worksheet, putting these results in Column C (the names should be in Column A and the results from Test 1 in Column B. Include a heading for the C column (i.e., put the phrase Test 2 in cell C1).
Now we want a chart showing both sets of results on the same diagram. Begin by selecting as usual all the cells from A1 to C11. Go through the procedure of creating the chart on a new sheet. Start by selecting Insert from the menu at the top of the screen, then select Chart from the drop-down menu, and finally select As New Sheet from the two Chart options which appear (this will, as we have gone through before, generate a new chart on its own page).
Excel will then go through the ChartWizard boxes again, until we have new bar chart, but this time one showing for each student's name (on the X-axis) two bars of different lengths and colours, one for Test 1 and one for Test 2. The Legend on the side of the chart will indicate which colour or shading represents which test.
We can edit this chart as before to add headings and a border and, if necessary, to change the shadings of the columns. If you are printing on a black-and-white printer, then you may want to experiment with different colour combinations to get the contrast you want on the final printed document.
If you are working with the chart directly on the Worksheet (with the columns of numbers), you can move the chart anywhere in the worksheet. Position the cursor in a blank area within the chart, hold down the left mouse button, and drag the mouse in the direction you want the chart to move. When you release the left mouse button, the chart will be in its new position.
V. Answers to Self-Test Exercises
Section C: Self-Test on Mode, Median, Mean
1. The "averages" for the salaries of the twelve Liberal Studies instructors are as follows: mean: $33,708.33; mode: $28,800; median: $30,600 (note that this is the average of the two middle salaries, since there is no value clearly in the middle). In this situation, since one of the figures is much higher than the others, the mean is somewhat misleading as an indication of a reliable average. The median or the mode would be more accurate.
2. The "averages" for the weights of the ten babies born are all the same: 8 lb.
Section E: Self-Test on a Simple Reading of a Histogram
Frequency Distribution B indicates values from 1 to 31. The most frequent values are at the ends of the distribution, and the frequency of the values is lowest at the central value (16). The decrease in the frequency from 1 to 16 matches the increase in the values from 16 to 31 (i.e., the distribution is symmetrical). The average value in this data will be at the centre, and its frequency will be low, the lowest in the frequency distribution.
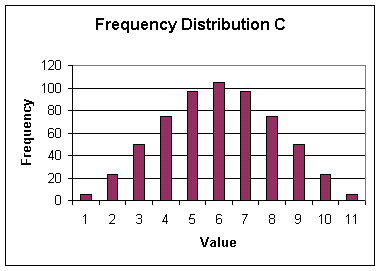
Frequency Distribution C indicates values from 1 to 11. Its shape is the reverse of Frequency Distribution C. Here the lowest frequencies are at the two extreme values, and the highest frequency is at the central value (6). The distribution is symmetrical, in the sense that the frequencies rise from the lowest up to the middle and then decrease from the centre to the highest values in such a way that the shape of the rising frequencies (to the left of the middle) matches the shape of the declining frequencies (to the right of the middle). The average value here will fall in the centre (6); this will also be the most frequent value.
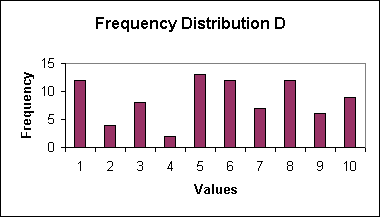
Frequency Distribution D charts the frequency of values from 1 to 10. There is no clearly discernible pattern to the distribution. Thus, it is difficult from a visual inspection to ascertain where the mean value might fall.
Section K: Self-Test on Standard Deviations and Excel Descriptive Statistics
Population A has a mean of 12.5 and a Standard Deviation of 6.13; Population B has a mean of 9.27 and a Standard Deviation of 4.05. Population A is thus more widely distributed that Population B.
Section N: Self-Test on z-Scores
In the first test (Test A) your mark of 81 is 5.5 above the mean of 75.5. Since the Standard Deviation was 12.44, your mark is 0.44 standard deviations above the mean (5.5 divided by 12.44); your z-score is therefore 0.44. In the second test, your score of 75 is 3 above the mean of 72. Since the Standard Deviation was 2.5, your z-score is 1.2 (3 divided by 2.5). Thus you did significantly better in the second test relative to the others taking the same tests.
Notes to Section Three
(1) In 1984 as part of its recruitment campaign the University of Virginia advertised that the graduates of its Department of Rhetoric and Communications had a mean starting salary of $55,000, a remarkably high figure. The high mean was the result of the fact that one graduate of the program, Ralph Sampson, had just signed a huge contract with an National Basketball Association team. The university did not indicate this (naturally), nor did it publish the median figure. In a recent baseball strike, the owners constantly talked about the $1.2 million average for big-league players (the mean). The players, in reply, pointed to the $400,000 median salary. Both sides used the term average. [Back to Text]
[Back to johnstonia Home Page]
Page loads on johnstonia web files
View
Stats
���������