Rock
drop site
How GPS Works
GPS consists of a constellation of 24 satellites in high orbit, over 20,000km, above the earth. These satellites were launched by the US military at a cost of over $12 billion, but are free to use. Accuracy varies from 10+ metres to fractions of a metre (used to be ~100 m error).
Close your eyes (ok, use your imagination). Imagine a rock being dropped into a lake on a calm day. A circular ripple expands and travels outwards from the point where the rock was dropped. Let’s say the ripple travels at a rate of 20 metres per minute. If you were in a boat and the ripple reached the boat in 8 minutes, the distance between the boat and the origin of the ripple could be calculated as 160 metres. This does not give you an exact location. The boat is somewhere on a 160m radius from where the rock was dropped.
Rock
drop site
Ripple
Now imagine a second location in the lake where a rock is dropped and that it takes 10 minutes for that ripple to reach you. You calculate that you are also 200m from the second source of ripples. You can be in one of two places.
Add a third circle (50m radius) and you have the exact location where all 3 ripples coincide.
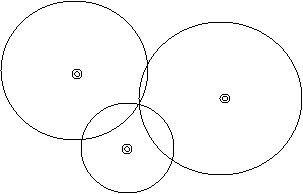
From Rocks to Satellites (formerly titled, From 2-D to 3-D)
This is the basic idea of GPS. Instead of ripples emanating from where rocks were dropped in the water, it is a radio signal emanating from many satellites. And you have to imagine this in three dimensions, not just two. My diagrams will be limited to 2 dimensions but the principles are the same. We locate our position relative to the known position of the satellites. If the 2 larger circles depicted above were ghost-like spheres that intersected each other, the intersection would not be one of 2 points (as above) but instead would be a circle of “exact intersection” (with part of each sphere intruding into the guts of the other). We would be located somewhere on the ring of this circle. We may want to narrow this down a bit. Add a third sphere (from a third satellite). The third sphere will intersect our “circle of intersection” at 2 points. Adding a fourth satellite would narrow it down to one location.
Remember in our boat on a lake scenario that we measured distance by measuring time. Since we knew how fast the ripple in the water was travelling, we only had to get a time measurement of when the ripple touched our location compared to when the ripple was first initiated. And we now know that for GPS radio waves are used. Radio waves travel at the speed of light (when in a vacuum, like outer space). Speed of light is 186,000 mph (297,600 km/hr). The time for a radio signal to reach earth’s surface from the satellites is about 0.07 seconds (you would obviously have to capture this measurement to many more decimal places). Very accurate clocks area required. In fact the satellites have atomic clocks. Actually they have 4 atomic clocks each (cost per clock is ~$100,000).
The satellites send out a digital signal (something like 0011010010111101010, only much longer). It is random in appearance (hence the name pseudo random code), but it is simply a very long code that repeats itself. The receivers are generating the same code at the same time. If the satellite and the receiver were beside each other, the code from the satellite would match, in time, the code of the receiver. With great distance between the receiver and satellite there is a slight delay in the satellite’s code as it has to travel through space. It’s this time difference that is used to calculate distance.
i.e. at exactly 12:00 noon the codes for the receiver and the satellite are compared:
from receiver 0011010010111101010
from satellite 0011010010111101010
The codes are not “in sync” because of the time needed for the signal to travel from the satellite to the receiver. We measure the time difference by comparing known parts of the code from each of the radio signals. In the diagram above we would have to adjust the code from the satellite to match the code of the receiver. This time adjustment gives us our time difference, from which we estimate our distance from the satellite.
Error in Time
Obviously we have a problem if there is an error in time measurement. Guess what ... there are several reasons why we will get an error in our time measurement. These reasons will be discussed later. Thus an timing error is inevitable. However, (most of) the 'timing error' is consistent, i.e. the error is the same for readings from all the satellites.
Refer to the diagram below. The skinny lines represent an accurate measurement. The fat lines represent “circles of location” but with a time error. Note that the true location (intersection of the skinny lines) lies with in a “triangular area” defined by the fat lines. As the error is consistent between the three satelittes, all three circles should be adjusted by the same time. In this case the fat circles are too big, indicating that the time recorded was too big. If we play with the timing of the signal from all three satellites (i.e. reduce each by 0.00000001 second) we will eventually get an exact match. In effect we would reproduce the “correct” skinny circles.
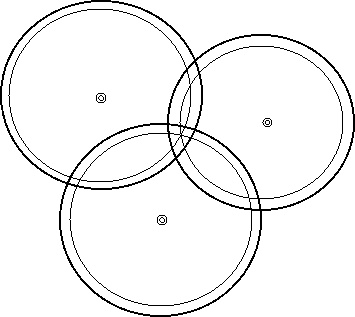
This proof was in 2 dimensions and shows 3 satellites. Remember that in real life (3-D) you would need 4 satellites. Summary: there are several sources of timing error - but this error is consistent. Thus we over come this error by adjusting the time from the satellites (all by the same time increment) until the true position is determined. This is done automatically in the GPS receiver.
Control Segment: There are 5 monitoring stations on earth that track the SV's to ensure they are in proper orbit. They send 'update data' to the SV's - this includes any adjustments to the atomic clocks and ephemeris data.
User Segment: These are simply the GPS receivers we use. They range from a few hundred dollars to tens of thousands of dollars. With regards to precision and reliability - well, you get what you pay for.
1. Clock error (1-2 m) – the diagrams above showed how error in the receiver’s clock is accounted for. The clocks in the satellites are accurate to the nanosecond. This however will still yield an error of a few metres.
2. Ephemeris (wobble) (2-3 m) – GPS determines your location in relation to the known location of the satellites. The exact location of the satellites is important. They do have a known orbit. However, energy pulses from the sun can affect their orbit. So the military monitors the location of the 24 satellites. When they get wobbled off course (ever so slightly), the military sends a signal to the satellite. The orbit is not adjusted, rather it’s true position is transmitted to earth. So the receiver gets 2 signals: the code for timing and a second signal that gives it’s true location.
3. Receiver (0.5m) – aside from clock error, there are various hardware design limitations. You get what you pay for. A GPS for a couple hundred dollars will not be as accurate as one that costs tens of thousands of dollars.
4. Ionosphere and Troposphere (5 m & ½ m, respectively) – the ionosphere is a charged layer of atmosphere surrounding the earth. Inside of this is a water-laden layer that literally “rains on our parade”. Both these layers affect the radio signal being sent from the satellites. The ionosphere tends to stretch the signal, whereas the troposphere shrinks it. The affect of the ionosphere can be calculated fairly well. The affect of the troposphere is more difficult as it requires a good measure of how much moisture is in the air (and this continuously changes).
5. Multiple-Path Error (1 m) – signals can be reflected (bounced off things), refracted (bent as it travels through something, like a forest canopy) or attenuated (delayed). Thus the receiver can receive more than one true signal from a satellite. If the receiver cannot determine the true signal (which should have got there first), then it will not use that satellite.
6.
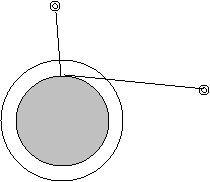PDOP
(Position Dilution of Precision) (factor ranges, 3-6)– what the $%#@ does
that mean? Simply put, the position of the satellites can affect the precision
of the answer. This error magnifies the others (i.e. a PDOP of 5 would magnify
each of the previous answers by a factor of 5). Two reasons spring to my mind.
Radio signals from satellites low on the horizon will have to travel for a
longer distance through the ionosphere and troposphere, hence increasing
uncertainty (as per item 4. above). Note that the signal from the overhead
satellite has a shorter distance to travel through the iono/troposphere than the
satellite 'low on the horizon'.
Satellites spaced well away from each other will yield a “crisper” intersection than satellites that are closely spaced.
7. Selective Availability (used to be ~100+ m, now it is 0 m) – this used to be the big one. However, now it is no longer an issue. Remember the military is involved in this. So to be sure that “unfriendlies” were not able to determine locations as well as they could, the military “dithered” the signal from the satellites. Basically they ensured the signals (timing and location) sent by the satellite to the world at large were not as accurate as the signals they used.
Differential correction can fix most errors, including selective availability.
If you had a GPS unit and sat in a chair out in the parking lot (basically with unknown coordinates) and received signals for say one hour, the coordinates received would vary over time due to the errors described above. If you were to plot these coordinates it would appear as though you were moving about the campus for that hour.
Now imagine that you had a GPS receiver at a known location. The coordinates you receive would still 'jump about' like the parking lot receiver, BUT you know your true location this time. This means you could determine the correction between your know location and the 'GPS location'. This correction is differential correction and can be applied to other GPS locations in your area - i.e. you would apply the differential location to the parking lot coordinates to get a true (or corrected) location.
It is important to note that we need to utilize readings from the same satellites at same time in order for this to work. There are many vendors and institutions that provide this service. In fact, with differential correction, even inexpensive receivers can yield locations to less than a metre.
There are 24 GPS satellites in orbit around the earth. We need 4
satellites to get a 3 dimensional fix.
Radio signals (pseudo random code) emanate from the
satellites and travel very fast (186,000 mph).
Measurement of time is very important. The satellites have 4
atomic clocks that cost $100,000 each. Receivers, needless to say, have cheaper
clocks. By adjusting the time period for all 4 satellites we can correct for a
cheap clock in the receiver.
The atomic clocks can still have a slight error (it gets corrected
when noticed by the military)
The exact location of the satellites is important. Their orbit is
fairly stable, but sometimes they wobble off their predicted course. So the
military monitors the exact location and sends up information that gives their
true position. In addition to the radio signal (called pseudo random code),
satellites send a second signal for their location.
Receivers have varying degrees of accuracy; the expensive ones are
more accurate, reliable and robust.
The charged ionosphere and water-laden troposphere affect the
timing of the radio signals.
Forest
canopies can affect the signals, resulting in the receiver getting many signals
from the same satellite.
For optimal precision, satellites should be high over the horizon
and well spaced from each other.
The military has the ability to “dither” with the signals from the
satellites. But this has not been done for some time.
Differential correction utilizes a known location to correct these
errors in the roving unit.