Help with Determining Area of Polygons
Area is a ‘square measure’ for the flat surface of a shape (or polygon). The area for a square or rectangle is simply calculated by multiplying length by width (e.g. 4 cm width * 9 cm length = 36 cm2). But what if an area has an irregular shape? Take a look at the polygon below.

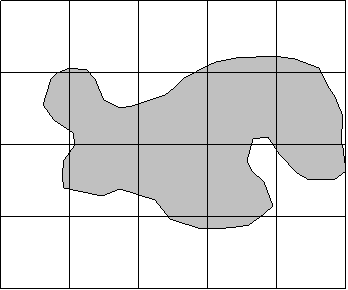
A simple formula does not exist that will determine the area of this shape. Instead, s simple and common method is to visualize an irregular shape as being made up of many small squares. We would then simply count the squares. The area of one square times the number of squares would give us a measure of area.
Seven of the squares are mostly occupied by the polygon. Squares occupied with less than 50% of the polygon are not counted. Obviously, using smaller squares would yield a more accurate estimate. But for this example, the large squares will suffice to show the method for determining area.
Now, what we really want to know is the land area (not map area) of the polygons. So we need to convert the squares to "real world dimensions". In our example assume the squares are the UTM grid (measuring 2 cm by 2 cm) and the scale of the map is 1:50,000. Therefore:
|
one edge of the square is 2 cm (map) * 50,000 = 100,000cm (real world) | |
|
this converts to 1,000 m along one edge | |
|
land area of one square is 1,000m * 1,000m = 1,000,000m2 | |
|
which converts to 100 ha (1,000,000 m2 / 10,000 m2 per ha) for each square |
So the real world area estimate would be 7 squares * 100 ha/square = 700 ha.
Getting a better answer ...
Note that in our example not one square was completely occupied by the polygon. But we did tally the 7 squares there were 'dominated' by the polygon. In each of these squares a portion was not occupied by the polygon. We 'hope' that the squares that have <50% of polygon coverage, which we did NOT count, balance this out. So how do we get a 'better', more reliable answer?
|
One way is to use smaller the squares. Using smaller squares provides for a 'finer resolution' and the more likely our answer will be more precise. | |
|
A second way is to 'multiple counts'. This means laying the graph paper over the polygon a few times and averaging the count. |
To get 'multiple counts' simply cast the graph paper over the polygon again. It will align differently than the first time. Obtain a second count. Average it with the first count. A second attempt is shown below.
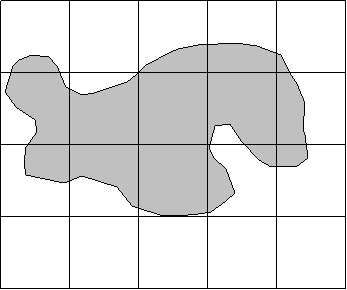
From this image we get a count of 6 squares - for an area of 600 ha. If we average with our first attempt we get 6.5 squares for a total of 650 ha.
Note that a 'tricky way' of getting multiple counts is to use the 'line intersections' as an additional count. In the first diagram we get a count of 7; in the second diagram we get 7 again. If we add these tallies of 'intersections' to our tallies of squares we get 7 + 7 + 7 + 6, which totals 27. Divide by 4 and we get 6.75 "squares", which equates to 675 ha.
Dot Grid
The dot grid is equivalent to graph paper. Counting each dot is equivalent to counting squares. Refer to the diagram below. Obviously you imagine that you have either graph paper OR a dot grid. The image below shows both together.

The benefit of a dot grid is that you do not have to debate whether a square is more or less than 'half covered' with the polygon (undoubtedly you did this when you were counting the squares earlier). You simply count the dot if it is "in" the polygon. For dots that are 'right on the border', well you can do one of two things (which amount to the same in the end):
| count every other one as being "in" the tally, or | |
| count each 'border dot' as half a dot. |
A note to the wise ... when you use graph paper and count the 'line intersections', you are essentially converting the graph paper to a dot grid.